Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
Loading...
In Varphi, head movement directions are represented using uppercase letters:
L : Move left
R : Move right
The characters "l" and "r" (lowercase "L" and "R") are not interpreted as "left" and "right" by the lexer, and will result in a syntax error.
In Varphi, a tally represents a tape cell containing a tally and is denoted by the character 1. A blank represents an empty tape cell and is denoted by 0.
The concept of a blank in Varphi is not to be interpreted as adding a new possible tape character. In the strictest sense, there is only one possible character in the alphabet of Turing machines, and that is a tally (given by 1 in Varphi). But if a tally is not present in a tape cell, then that tape cell is blank (represented using 0 in Varphi), and does not contain any tape character.
A line represents a transition rule in the Turing machine. Every line consists of five elements in the following order:
A state name representing the current state of the Turing machine.
A tally or blank representing the condition of the tape cell that the head is currently positioned at.
A state name representing the state the Turing machine is left in after the transition is applied.
A tally or blank representing the condition of the tape cell after the transition is applied.
A head direction representing the direction the head will move in after the transition is applied.
A general line will look like the following:
The space between elements of a line is not restricted to being a single space. Any whitespace can be added between elements of a line without causing syntax errors, which makes it possible to format programs!
The parser uses the following pattern to match lines (assuming single spaces between elements, though this is not required):
The first two elements of a Varphi line are called the condition. The condition can be read as follows:
If
the Turing machine is using state [state], and
the tape cell which the head is currently situated at [contains a tally/is blank]
The remaining three elements of the line are called the instruction. They instruct the Turing machine to perform a series of actions. You can read the instruction as follows:
Make
the Turing machine use state [state]
the tape cell at the which the head is currently situated at [contain a tally/blank]
the head move to the tape cell immediately to the [left/right] of the tape cell which it is currently situated at.
Overall, you can read a Varphi line as follows:
If
the Turing machine is using state [state]
the tape cell which the head is currently situated at [contains a tally/is blank],
then make
the Turing machine use state [state]
the tape cell at the which the head is currently situated at [contain a tally/blank]
the head move to the tape cell immediately to the [left/right] of the tape cell which it is currently situated at.
A state name in Varphi starts with the letter q, followed by at least one alphanumeric character or underscore (_).
Examples of valid state names include:
q0
qzero
q_My_State_
q_my_state__
The lexer uses the following pattern to match state names:
Comments enhance code readability by providing explanations and context. They can also be used to temporarily disable code when testing alternate code.
Varphi conveniently uses C-style comments. There are two types of comments in Varphi:
Inline (single-line) comments
Block (multi-line) comments
An inline comment begins with //. Any text following // on the same line is ignored by the compiler and does not affect execution.
Inline comments can appear on lines of a source file by themselves:
Inline comments can also appear at the end of a Varphi line:
A block comment begins with /* and ends with */. Any text enclosed within these markers is ignored by the compiler. Block comments are useful for providing detailed explanations spanning multiple lines.
Here's an example of a block comment spanning multiple lines:
Varphi programs are extemely simple. They consist of lines, separated by newlines. They can also include comments.
Varphi supports both deterministic and nondeterministic Turing programs. Nondeterministic programs have two or more lines with the same condition, but with different instructions.
The Varphi Interpreter does not explicitly check for a particular extension for input files. However, it is considered a good practice to use the .vp extension anyways.
For this guide, we'll use the Varphi program that we created from the last section, where we add two positive integers. For your convenience, we have included it below (the version without comments):
The first step is to create a file and save this code to it. We'll assume the file's name is add.vp , but feel free to name it anything you wish!
Remark: The Varphi Interpreter does not produce any output when you execute it on an input program, since it will be waiting for the input tape on standard input. No prompt appears that asks for this. It is common to confuse this as the interpreter "loading" or "hanging," when in reality it is just waiting for the input tape.
Now recall the output convention from the last section:
The Varphi interpreter automatically prints out all tape cells that have ever been accessed. This includes tape cells that have been written to (even when writing the input tape) and read from.
Arguably the only ambiguity in a Varphi program is the starting state. How is the state which the Turing machine starts with determined?
The "Top-Left" Rule is a rule that can be applied to determine the starting state of any Varphi program. Simply select the state located at the top-left corner of the program. For example, suppose your program looks like this:
Then, the starting state is q0.
Input tapes must include at least one tape cell with a tally. If not, a runtime error will be thrown.
This guide assumes you have already have the Varphi Interpreter (vpi) installed on your machine. If not, please refer to the .
We'll now run this program on our example from the last section, where we added and . To do so, run the following command
You should notice that no output is produced, for the interpreter is waiting for you to provide the input tape. Since we're adding and , the input tape is 111011 (remember, 0 represents a blank tape cell, not a tape cell with the character "0"). Type this string into your terminal and hit ENTER. The output tape should then be printed on the terminal.
There shall only be one contiguous block of tallies, which will represent the output of the Turing machine. If there are tallies in the contiguous block, then the number being represented by the tape is .
Under this output convention, the output tape, 000011111 , represents the decimal number , which is a correct result (as )!
A standard that is followed by Turing machine developers is to make the initial position of the head be the leftmost tally on the tape. This convention is adopted by Varphi. The leftmost tally is guaranteed to exist by the .
Writing Varphi programs is not like writing programs in other languages, since it uses a completely different paradigm. It is very easy to write the wrong state name in the instruction part of a line, or to have incorrect logic somewhere. When things do go wrong, you can debug your code with Varphi.
The Varphi Command-Line Debugger ships with the Varphi interpreter, and can be used by supplying the -d option to vpi . We'll continue to use our running example of the addition program from this section.
Let's run the Varphi program in debug mode. Run the following command
Again, you should see no output, since you must supply the input tape first. Let's do that:
The debugger shows you the current state, as well as some details of the tape. You may notice the square braces [] and curly braces {} . These are explained below:
Square braces [] around an element of the tape indicate that the head is currently stationed at that tape cell.
Curly braces {} around an element of the tape indicate that this tape cell was the tape cell which held the first tally in the input tape. It can be used as a "reference point" when debugging.
As you can see from the output of the debugger, you can step through the program by pressing ENTER. When the program finishes executing, the output tape will be printed and the debugger will exit.
In case you're interested, here's the whole session output for this debugger run:
Below is a program that adds one tally to an input tape (which, by the "At Least One Tally" Rule, must contain at least one tally)
Below you can find some more examples of Turing machines described using Varphi.
Addition By One
Add Two Numbers
Multiplication By Two
Rock, Paper, Scissors
Coin Flip
Below is a Varphi program that adds (i.e., "merges") two contiguous blocks of tallies (containing at least one tally each) separated by a blank tape cell into one contiguous block of tallies.
From our example in this section, it is clear that writing comments to explain what each state does is important for readers to understand your programs.
To document a state, you should open a block comment before it and try your best to explain the following details:
The purpose of the state
What the machine does if a tally is encountered at the current tape cell when on the state
What the machine does if a blank tape cell is encountered at the current tape cell when on the state
When possible, try to limit the number of states your Varphi program uses to avoid a large file. This may be accomplished by moving to a simple algorithm. This is a concept that is applied in every other programming language (although not necessarily with state names like in Varphi, but perhaps with variables).
State names can follow any identifier naming case style you prefer. However, you should ensure that the names of your states are clear, especially in larger programs, as the number of states required by algorithms tends to grow extremely fast as the algorithms become more complex.
Files should be given a name that is descriptive of the Turing machine they represent, and should end with the .vp extension.
The .vp extension is not a requirement for Varphi files, but it is conventional to give Varphi files this extension.
On a Varphi line where you are transitioning to a halting state, pay attention to the direction you move the head before halting. If possible, move the head in a direction such that its final position will be an already-visited tape cell. If you move the head in a direction such that its final position is not an already visited tape cell, then that tape cell will be considered visited, and will be displayed in the output tape (the Varphi Interpreter will automatically display all visited tape cells in the output tape).
Below is a program which determines the winner of a game of Rock, Paper, Scissors between two players.
The machine accepts an input tape containing two contiguous blocks of tallies separated by a blank tape cell, representing the moves of the two players. The first block of tallies (i.e., to the left) will represent the move of the first player, and the second block will represent the move of the second player.
Each contiguous block for a player's move can look like the following:
1 , if the move is Rock
11 , if the move is Paper
111 , if the move is Scissors
For example, the input tape 110111 would represent that the first player played Paper, and the second player played Scissors.
The output tape will be a contiguous block of tallies representing the result of the game. This output tape will take on one of the following forms:
1 , if the result was a tie
11 , if the first player won
111 , if the second player won
Below is a program accepting a single contiguous block of tallies (containing at least one tally) and duplicates it. The output tape will be a contiguous block of tallies containing double the tallies in the original contiguous block of tallies on the input tape.
Let's get started with Varphi and write a program from scratch.
The objective of this tutorial is to show how to write a simple program with Varphi. We will show how to go about thinking about the algorithm, and then how to translate that algorithm into Varphi.
The Turing machine we will design for this guide performs binary addition (that is, addition of two numbers), specifically on numbers from the set of positive integers, in a more unique way (a very efficient way is given here).
The input tape's representation convention will be as follows:
To represent two positive integers and , repeat tallies, followed by a blank, followed by tallies. Leave the rest of the tape blank.
The output tape's representation convention will be as follows:
There shall only be one contiguous block of tallies, which will represent the output of the Turing machine. If there are tallies in the contiguous block, then the number being represented by the tape is .
When thinking about how to design Turing machine algorithms, it often helps to think about an example. Suppose we would like to add the positive integers and . Under the input representation convention, the input tape to the machine will look like the following:
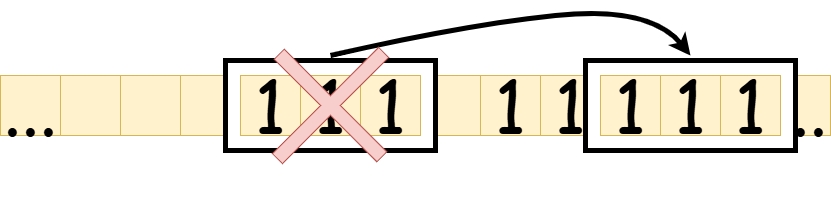
We would like to "merge" these two numbers to form a contiguous block with five tallies on it. One may think about this as perhaps shifting all the tallies of the left (or right) number to the right (or left) by one tape cell. The way we will implement it is by "teleporting" the left (or right) number to appear immediately to the right (or left) of the right (or left) number. This is depicted below. Again, this is by no means the most efficient way to do this, but we implement it in this way for demonstration purposes.
A way to perform such an algorithm is to transfer each individual tally to the left of the right number, one-by-one. That is, for every tally in the left number, delete it, then go to the rightmost tally of the right number and replace the blank cell to the right of it with a tally.
Let's phrase this in a more "Turing-machine-like" way. For the purposes of this algorithm, let's call the blank tape cell separating the two numbers on the input tape the middle blank. Now recall that the Turing machine's head always starts off at the leftmost tally. So, what we'll do is replace that tally with a blank, then pass all of the remaining tallies of the left number (moving the head to the right) until we hit the middle blank. Once we hit this middle blank, we'll skip it, then skip all of the tallies of the right number (again, still moving the head to the right) until we hit the first blank to the right of the right number. Then, write a tally to this blank tape cell. Now we have successfully transferred the first tally of the left number to the right place. To start working on the rest of the tallies of the left number, skip through the tallies of the right number (moving the head left this time) until we hit the middle blank. Once we hit the middle blank, we'll skip it, then skip all of the tallies of the left number (again, still moving the head to the left) until we hit the first blank to the left of the left number. Then, move the head one position to the right. If the tape cell at this tape cell is blank, then we've successfully moved all the tallies of the left number to the right of the right number. Otherwise, we still have tallies to move, and we can restart the same process we took with the initial tally we moved.
Hopefully this algorithm makes intuitive sense. However, notice how much it took us to describe it in English. Below, you'll see the equivalent Varphi algorithm, and you can judge for yourself if it makes writing such algorithms easier!
Now that we have an algorithm, we can start to write it in Varphi. You may be able to see from the algorithm's description that we need six states:
A state for replacing the leftmost tally of the left number with a blank
A state for skipping the tallies of the left number, moving towards the right
A state for skipping the tallies of the right number, moving towards the right
A state for skipping the tallies of the right number, moving towards the left
A state for skipping the tallies of the left number, moving towards the left
A halting state
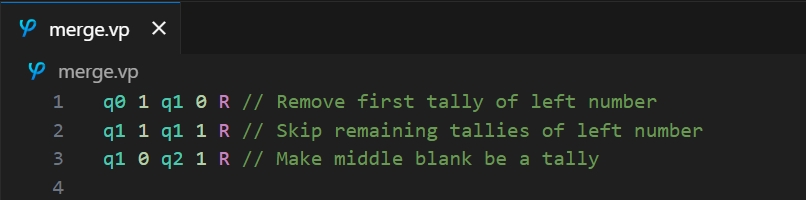
Instead of describing in English the function of each state and how it connects with other states, we've decided that a Varphi program may actually be the clearest way to do this. Here's the Varphi program describing this Turing machine:
Here's a version without comments:
In the context of a Turing machine, the tape is a component that serves as a place to store information. The tape can be thought of as as paper that is divided into squares, which we will refer to as tape cells. Each tape cell can either
Be left empty
A special thing about the tape, and also one of the reasons why Turing machines are strictly theoretical, is that it spans infinitely. That is, there are infinitely many empty tape cells spanning in both directions.
Since we now have access to the concept of blank tape cells on our tape, we can also use such blank tape cells in our representation conventions. For example, here's a representation convention that allows for representing multiple numbers on the tape:
We use the terms "a blank tape cell" and "a blank" interchangeably in this text.
With Turing machines, a restriction is placed on the initial state of the tape. It must contain at least one tally initially. Therefore, when choosing your representation convention for some domain, ensure that all elements of the domain can be represented using at least one tally.
To make development easier for those who prefer a graphical environment over a command-line, a language extension was developed for Microsoft's Visual Studio Code (VS Code). This document shows how to use the extension to enable Varphi development in VS Code.
The extension will only recognize files with the ".vp" extension as being Varphi files. Thus, please ensure you name your Varphi files with this extension.
Once you create a Varphi file and open it in VS Code, you should see several indicators that the extension is functioning properly. The first of these is that the file should be given a unique icon in the file's tab and in the explorer panel. For example, here's how the tab of a file named "merge.vp" will look like:
And here's what it will appear as in the explorer panel:
Another indicator is that the language mode (usually displayed in the bottom-right corner of the window) will indicate that the current language mode is "Varphi":
The third indicator is that there will be two buttons in the top-left of the window.
These buttons allow for debugging and running the current program, respectively.
The final indicator is that the source code will be colored. For example:
With a Varphi file opened, click the "Run Program" button in the top-left corner of the window, shown below
You will then be prompted for the input tape:
After inputting this and pressing Enter, you may (if this is your first time using the extension) receive a prompt asking for the path to the Varphi Interpreter. Please input the path to the vpi binary you installed earlier.
IMPORTANT: When entering the path to the Varphi Interpreter, do not use quotes. Also, please input the complete path to the executable and not just the parent directory of the executable.
If you need to change the path to the Varphi Interpreter in VS Code (which will be saved after the first time you input it), go to File -> Preferences -> Settings, then search for "varphi", and you should see the following setting:
You can enter the new path here to overwrite the saved one.
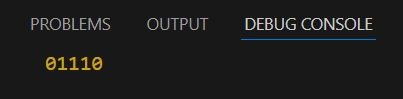
Next, click View -> Debug Console to open the Debug Console, where the output tape will be displayed:
Varphi's VS Code language extension provides a graphical debugging interface, enabling stepping through Varphi programs line-by-line.
To get started, open a Varphi program in VS Code and press the "Debug Program" button:
You will then be prompted for the input tape:
After inputting this and pressing Enter, you may (if this is your first time using the extension) receive a prompt asking for the path to the Varphi Interpreter. Please input the path to the vpi binary you installed earlier.
Next, from the side-menu, open the "Run and Debug" panel:
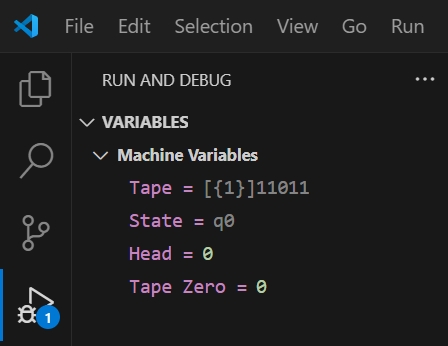
Now expand the VARIABLES -> Machine Variables menu in the "Run and Debug panel, and you should see the following variables:
Here's an explanation of each variable:
Tape: Shows each tape cell. 1 means that tape cell has a tally, and 0 means that tape cell has a blank. The tape cell that held the leftmost tally of the input tape will be surrounded by curly braces ({}). The tape cell that the head is currently stationed at is surrounded by square brackets ([]).
State: The name of the current state of the machine.
Head: The index (0-indexed) of the tape cell that the head is currently positioned at. It is a redundancy with the square bracket notation in the Tape variable.
Tape Zero : The index (0-indexed) of the tape cell that held the leftmost tally of the input tape. It is a redundancy with the curly brace notation in the Tape variable.
You will also notice that the source code has a line highlighted in yellow:
When a line is highlighted like this, it means that the line's condition applies, and its instruction will be executed after the next step.
To step the program, you should use the "Step Over" button in the debug options:
You can restart the debugging session with the "Restart" button:
You can stop the debugging session with the "Stop" button
The Varphi VS Code extension also supports setting breakpoints for debugging sessions. To do this, you can (before starting the debugging session) hover to the left of the line(s) you wish to set a breakpoint at in the Varphi source and then click the red dot:
After clicking, the red dot should persist (until you click it again, which will remove it):
Now, simply start debugging your program as normal, and you'll notice that the first highlighted line will be one of the lines you set a breakpoint at:
From here you can step through the code using the "Step Over" button as before and possibly hit lines that aren't breakpoints. But if you'd like to jump to the next breakpoint, you can use the "Continue" button:
That's it! You've just written your first Varphi program
Below is an example of a Varphi program that, when given an input tape containing exactly one tally, returns an output tape containing one or two tallies.
Contain a tally (i.e., )
We can use the tape as a means of representing numbers. Since tape cells can only contain the symbol if they are not left blank, we will have to use the unary number system to represent numbers. For example, here's a representation of a tape containing the decimal number , assuming the representation convention is to repeat times to represent a number .
As you can see, we represented the decimal number by writing seven s side-by-side. On the left and right of the number are infinite tape cells that are blank.
To represent a multiset of positive integers , write s, followed by a blank, followed by s, followed by a blank, and so on...
Here's a representation of a tape containing the two decimal numbers and :
This document assumes that you have the extension and all its prerequisites installed. To view installation steps for the language extension, please view the .
From Wikipedia:
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
There are infinitely many number systems. The most commonly used of these is the decimal (base 10) number system, which uses the symbols to represent numbers. Our modern-day computers use the binary (base 2) number system, which uses the symbols and to represent numbers. For example, the binary representation of the decimal number is .
By definition, the simplest number system is the one which uses the least number of symbols. This number system is called the unary number system, and it uses one symbol to represent numbers, which we call a tally.
We will often use the symbol to denote a tally in this text.
You use this number system more than you know! Imagine trying to represent the decimal number on your fingers. You would put up seven fingers (probably, unless your brain operates in binary), which is like writing seven tallies on a paper!
Although the unary number system is extremely simple, it is not any less (or more) powerful than any other number system.
The example above about representing numbers on your fingers shows how to use the unary number system to represent positive numbers. This does not mean that the unary number can only represent positive numbers, however.
In the above example, the following representation convention was used
To represent a number , repeat the symbol times.
Suppose now that we wanted to represent the set of nonnegative integers (to be able to represent zero as well) using the unary number system. We could define the following representation convention:
To represent a number , repeat the symbol times.
Above, we used to represent the set of nonnegative integers (i.e., .
Under this representation convention, we can represent the number decimal number with , the decimal number with , and so on...
You can theoretically come up with any convention you like to represent a set of numbers using unary. Here's a rather crazy one:
To represent a number , repeat the symbol times.
Try to represent the decimal number in unary using this convention.
The whole point of this is to show that providing a unary representation of a number to someone is not enough for them to know which number is being represented. You must also give them the convention you used to come up with that representation. The number that the unary representation represents varies greatly between the three input conventions shown above (it represents six, five, and one respectively).
The Turing machines discussed in this section so far, such as the one that adds two tallies to any number, are called deterministic machines, since their outputs are guaranteed to be the same every time if the input tape is the same between runs.
Turing machines can also be nondeterministic, meaning their outputs can vary between runs with the same input tape.
For example, consider the following transition function (written as a Turing program, or Varphi program):
Notice that we have defined two different rules for when the Turing machine is on state qStart and encounters a tally. The first rule instructs the Turing machine to leave the tally untouched and halt, while the other rule instructs it to make the tape cell blank and halt.
Which path will the Turing machine take on an input tape with one tally? There is no way to tell. The machine actually has a 50% chance of using the first rule over the second, and vice versa. So, for one run of the machine, the output tape may have one tally, and for another run, it will have no tallies.
Wow! That's a lot to take in. The first three items in the quadruple are pretty straightforward, but what is that fourth item? Let's describe this in a more gentle way:
Recall our example of adding two tallies to a number on a tape. We used the following algorithm:
The transition function for this algorithm can be represented using a table:
We can write the transition function in an even more compact notation as follows:
Believe it or not, you've just written your first Varphi Program! Here it is in a code block.
Pretty simple, right?
A Turing machine is a quadruple , where
is a finite nonempty set of states (e.g., , for some .
is the initial state.
is the set of final states.
is the transition (partial) function.
NOTE: Above, we represent "tally" using , "blank" using , "left" using , and "right" using .
is a partial function (may not be defined for some inputs in the domain) mapping pairs of non-final states and tape cell possibilities to triples containing a state, tape cell possibility, and head direction.
For example, if maps to , then this can be read as "if the machine's state is and the current tape cell is blank, then switch to state , place a tally at the current tape cell, and move the head to the tape cell immediately right of the current tape cell.
Since we previously mentioned that states do not need to define rules for all possible tape cell conditions, is a partial, not total, function.
Start at state . Read the current tape cell.
If we are on state :
If there is a tally at the current tape cell, write a tally to the current tape cell (leaving it as-is) and move to the tape cell immediately to the right of the current one. Stay on state . Repeat.
If the current tape cell is blank, write a tally to the current tape cell and move to the tape cell immediately to the right of the current one. Switch to state . Repeat.
If we are on state :
If the current tape cell is blank, write a tally to the current tape cell and move to the tape cell immediately to the right of the current one. Switch to state . Repeat.
Again, means "tally", means "blank", means "right", and means "left" here.
The transition function of a Turing machine is extremely powerful. In fact, supplying just the transition function of a Turing machine gives you everything you need to know about the Turing machine except for the initial state of the machine. However, we will make the assumption that the initial state is the first state mentioned (that is, the state at the top left corner of the Turing program), which is called the . Writing the transition function in compact notation makes it very easy to describe Turing machines without heavy notation or tables.
0
In the context of a Turing machine, the head is a component that can read from, write to, and traverse the tape.
The head is restricted to being stationed at exactly one tape cell at a time. That is, it cannot read or write a block of cells (more than one cell) at one time. Additionally, the head cannot "teleport" to a certain tape cell that is not immediately to the left or right of the tape cell it is currently stationed at. It can only move to the left or to the right by exactly one tape cell at a time.
As a device, the head can perform the following actions:
Read the current tape cell
Write a tally () to the current tape cell
Make the current tape cell blank
Move to the tape cell immediately to the right of the current one
Move to the tape cell immediately to the left of the current one
However, the head only accepts instructions that are in one of the following formats:
Read the current tape cell
Write a tally to the current tape cell and move to the tape cell immediately to the right of the current one
Write a tally to the current tape cell and move to the tape cell immediately to the left of the current one
Make the current tape cell blank and move to the tape cell immediately to the right of the current one
Make the current tape cell blank and move to the tape cell immediately to the left of the current one
The Turing machine will supply such instructions to the head as part of its operation.
To understand Turing machine states, an example is usually very helpful.
Suppose we are using the following representation convention:
To represent a number , repeat the symbol times.
Now suppose you are given the following tape:
You are tasked with making the tape, after you are done, contain one more tally () than what was originally on it. Specifically, you should add the extra tally to the right of the tallies that were originally on the tape. Also suppose that the only way you can access the tape is through a Turing machine head, which you control by supplying instructions to. The head will originally be stationed at the leftmost tally on the tape (which you can assume is guaranteed to exist). Also assume that there is exactly one contiguous block of tallies on the tape.
In the task description above, we stated that the head will be stationed at the the leftmost tally on the input tape. In Varphi, and in Turing machines in general, this is an assumption that holds. The head of a machine that is described using Varphi will always start at the leftmost tally on the input tape.
A natural way of doing this is as follows:
Read the current tape cell.
If there is a tally at the current tape cell, write a tally to the current tape cell (leaving it as-is) and move to the tape cell immediately to the right of the current one. Repeat.
If the current tape cell is blank, write to the current tape cell and move to the tape cell immediately to the right of the current one. Stop.
Now what if the task was to add two tallies instead of just one? Let's try to write a similar algorithm:
Read the current tape cell.
If there is a tally at the current tape cell, write a tally to the current tape cell (leaving it as-is) and move to the tape cell immediately to the right of the current one. Repeat.
If the current tape cell is blank, write a tally to the current tape cell and move to the tape cell immediately to the right of the current one. What now??? We still need to add one more tally.
It turns out that we don't have enough expressive power to achieve this task without introducing the concept of states.
We can think of a Turing machine state as being a "state of mind" of the Turing machine. For the example where we are adding two s to the right of a number, we can rewrite the algorithm using states as follows:
Start at state . Read the current tape cell.
If we are on state :
If there is a tally at the current tape cell, write a tally to the current tape cell (leaving it as-is) and move to the tape cell immediately to the right of the current one. Stay on state . Repeat.
If the current tape cell is blank, write a tally to the current tape cell and move to the tape cell immediately to the right of the current one. Switch to state . Repeat.
If we are on state :
If the current tape cell is blank, write a tally to the current tape cell and move to the tape cell immediately to the right of the current one. Switch to state . Repeat.
We have written our algorithm in a completely unambiguous way. Notice that not every state needs to define rules. For example, has no rules, which means it's a halting state (the algorithm terminates if we reach this state). Also, notice that defines no rule for if a tally is encountered at the current tape cell, because we do not expect there to be any non-blank tape cell to the right of the tape cell containing the rightmost tally of the input number.
